..\3C_02.md | Springli’s Blog

type

status

date

slug

summary

考试要求：

理解广义积分（无穷限积分、瑕积分）的概念，掌握无穷限积分、瑕积分的收敛性判别法，会计算一些简单的广义积分。

掌握用定积分表达和计算一些几何量与物理量（平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、截面面积为已知的立体体积、功、引力、压力）及函数的平均值

（3）反常积分

一. 考试内容要点

（一）无穷区间上的反常积分

（二）无界函数的反常积分

二. 常考题型方法与技巧

题型一反常积分的敛散性

题型二反常积分的计算

3.1 考试内容要点

3.1.1 无穷区间上的反常积分

定义1 ：

定义2

定义3

定理1 (比较判别法)

设

在

上连续，且

，则

收敛

收敛

发散

发散

定理2 (比较判别法的极限形式)

设

在

非负连续，

，则

时，

同敛散；

时，若

收敛

收敛；

时，若

发散

发散。

常用结论：

当

收敛，当

发散 (

)

3.1.2 无界函数的反常积分

定义1 设点

为函数

的瑕点

定义2 设点

为函数

的瑕点

定义3 设点

为函数

的瑕点 (

)

定理1 (比较判别法)

设

在

上连续，且

，则

收敛

收敛

发散

发散

定理2 (比较判别法的极限形式)

设

在

非负连续，

，则

时，

同敛散；

时，若

收敛

收敛；

时，若

发散

发散。

常用结论：

当

收敛，当

发散

Γ 函数

定义

递推公式

3.2 常考题型

3.2.1 题型一反常积分的敛散性

例1 下列反常积分发散的是

(A)

(B)

(C)

(D)

例2 反常积分

收敛，则 ( )

(A)

(B)

(C)

(D)

例3 设

均是正整数，则反常积分

的收敛性

(A) 仅与

的取值有关。

(B) 仅与

的取值有关。

的取值都有关系。

(D) 与

的取值都无关。

例设

为常数，若反常积分

收敛，则

的取值范围是 ( )

(A)

(B)

(C)

(D)

f(x) = \begin{cases} \frac{1}{(x - 1)^{\alpha - 1}}, & 1 < x < e, \ \frac{1}{x \ln^{\alpha + 1} x}, & x \ge e. \end{cases}

\int{1}^{+\infty} f(x) dx

(A)

(B)

(C)

(D)

3.2.2 题型二反常积分计算

(4) 定积分的应用

一、考点内容要点

（一）几何应用

（二）物理应用

二. 常考题型方法与技巧

题型一几何应用

题型二物理应用

4.1 考点内容要点

4.1.1 几何应用

1. 平面域的面积

y=f(x), y=g(x) (f(x) \geq g(x))

x=a, x=b (a < b)

若平面域

由曲线

所围成，则其面积为

2. 空间体的体积

1) 旋转体的体积

平面域

线直线

(该直线不穿过区域

) 旋转所得旋转体体积记为

2) 已知横截面积的体积

3) 曲线弧长

4) 旋转体侧面积

4.1.2 物理应用

物理应用

压力

变力做功

引力

4.2 常考题型方法与技巧

4.2.1 题型一几何应用

例1

设

，求曲线

与

轴所围图形的面积。

例2

设平面图形

由

与

所确定，求图形

绕

旋转一周所得旋转体的体积。

例3

过点

作曲线

的切线，该切线与曲线

及

轴围成平面图形

的面积

轴旋转一周所得旋转体的体积

轴旋转一周所得旋转体的体积

线直线

旋转一周所得旋转体的体积

例4

设对数螺线

及射线

和

围成平面图形

的面积

线极轴旋转一周所得旋转体的体积

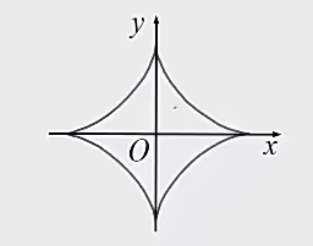
例5

设星形线

求

它所围的面积；

它的周长；

它绕

轴旋转而成旋转体的体积和侧面积。

4.2.2 题型二物理应用

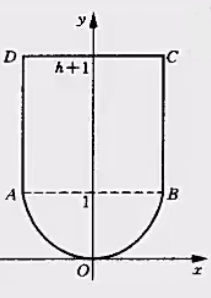
例1

某闸门的形状与大小如图所示，其中

轴为对称轴，闸门的上部分为矩形

，下部由二次抛物线与线段

所围成，当水面与闸门的上端相平时，欲使闸门矩形部分承受的水压力与闸门下部承受的水压力之比为5：4，闸门矩形部分的高

应为多少。

例2

一容器的内侧是由曲线

绕

轴旋转而成的曲面，其容积为

，其中盛满水，若将容器中的水从容器的顶部抽出

，至少需做多少功？ (长度单位：

重力加速度为

，水的密度

)