type
Post
status
Published
date
Aug 27, 2024
slug
summary
高数
tags
知识
category
知行合一
icon
password
一元函数积分学考试要求：（1）不定积分1.1 考试内容要点:1.1.1 两个基本概念1.1.2.原函数的存在性1.1.3.不定积分的性质1.1.4.基本积分公式1.1.5.三种主要积分法1.第一类换元法（凑微分法）2.第二类换元法3.分部积分法1.1.6.三类常见可积函数积分1.2 常考题型的方法与技巧题型一 计算不定积分题型二 不定积分杂例（2）定积分2.1.考试内容要点2.2.1 定积分的概念2.2.2 定积分的几何意义2.2.3 定积分的存在性2.2.4 定积分的计算2.2.5 变上限积分函数及其应用2.2.6 定积分的性质2.2 常考题型的方法和技巧2.2.1 题型一 定积分的概念、性质及几何意义2.2.2 题型二 定积分计算2.2.3 题型三 变上限积分函数及其应用2.2.4 题型四 积分不等式

一元函数积分学

考试要求：

  1. 理解原函数的概念，理解不定积分和定积分的概念。
  1. 熟练掌握不定积分的基本公式，熟练掌握不定积分和定积分的性质及定积分中值定理。掌握牛顿－莱布尼茨公式。熟练掌握不定积分和定积分的换元积分法与分部积分法。
  1. 会求有理函数、三角函数有理式和简单无理函数的积分。
  1. 理解变上限定积分定义的函数，会求它的导数。
  1. 理解广义积分（无穷限积分、瑕积分）的概念，掌握无穷限积分、瑕积分的收敛性判别法，会计算一些简单的广义积分。
  1. 掌握用定积分表达和计算一些几何量与物理量（平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、截面面积为已知的立体体积、功、引力、压力）及函数的平均值（1） 不定积分（2） 定积分（3） 反常积分（4） 定积分应用

（1）不定积分

考试内容要点：
（一）两个基本概念
（二）原函数的存在性
（三）不定积分的性质
（四）基本积分公式
（五）三种主要积分法
（六）三类常见可积函数的积分
常考题型方法与技巧：
题型一 计算不定积分
题型二 不定积分杂例

1.1 考试内容要点:

1.1.1 两个基本概念

  1. 原函数：
  1. 不定积分：

1.1.2.原函数的存在性

  1. 若
  1. 在区间
  1. 上连续，则
  1. 在区间
  1. 上必有原函数；
  1. 若
  1. 在区间
  1. 上有第一类间断点，则
  1. 在区间
  1. 上没有原函数；

1.1.3.不定积分的性质

1.1.4.基本积分公式

1.1.5.三种主要积分法

1.第一类换元法（凑微分法）

若
，且
可导，则

2.第二类换元法

设函数
可导，且
，又设
则

3.分部积分法

设
有连续一阶导数，则
注：
1.适用两类不同函数相乘
  1. 比
  1. 好积

1.1.6.三类常见可积函数积分

  1. 有理函数积分
  1. 一般法（部分分式法）特殊方法（加项减项拆或凑微分）
  1. 三角有理式积分一般方法（万能代换）
特殊方法（三角变形，换元，分部）:
  1. 若
  1. ，则
  1. 若
  1. ，则
  1. 若
  1. ，则
3.简单无理函数积分
令

1.2 常考题型的方法与技巧

题型一 计算不定积分

例1
例4
例7
例8
例10
例11
例13

题型二 不定积分杂例

例1 若
求
例2 若
为
的一个原函数，求
例3 设
为
的原函数，且当
时，
已知
。求
.
例4 设
求
.
例5 求不定积分

（2）定积分

1.考试内容：
（一）定积分概念
（二）定积分的几何意义
（三）可积性
（四）定积分的计算
（五）变上限积分
（六）定积分的性质
2.常考题型方法与技巧
题型一 定积分的概念、性质及几何意义
题型二 定积分计算
题型三 变上限定积分函数及其应用
题型四 积分不等式

2.1.考试内容要点

2.2.1 定积分的概念

注：

2.2.2 定积分的几何意义

2.2.3 定积分的存在性

  1. 必要条件：
  1. 有界；
  1. 充分条件
    1. 在
    2. 上连续；
    3. 在
    4. 上有界且只有有限个间断点；
    5. 在
    6. 上仅有有限个第一类间断点。

2.2.4 定积分的计算

  1. 牛顿-莱布尼茨公式
  1. 换元积分法
  1. 分部积分法
  1. 利用奇偶性和周期性
例 设
，k 为整数，则 I 的值
(A) 只与 a 有关。
(B) 只与 k 有关。
(C) 与 a, k 均有关。
(D) 与 a, k 均无关。
  1. 利用公式

2.2.5 变上限积分函数及其应用

定理 设
在
上连续，则
在
上可导且
例1 设
连续，试求下列函数的导数

2.2.6 定积分的性质

  1. 不等式
    1. 若
    2. ，则
    3. 。
    4. 若
    5. 在
    6. 上连续，则
  1. 中值定理
    1. 若
    2. 在
    3. 上连续，则
    4. 若
    5. 在
    6. 上连续，
    7. 不变号，则
例2 设
在
上连续，在
内可导，且
求证：在
内至少存在一点
使得
。

2.2 常考题型的方法和技巧

2.2.1 题型一 定积分的概念、性质及几何意义

例1 求
例2 设
连续, 且
则
例3 求极限
例4 如图，连续函数
在区间
上的图形上的图形分别是直径为1的上、下半圆周，在区间
上的图形分别是直径为2的下、上半圆周(图)，设
, 则下列结论正确的是：
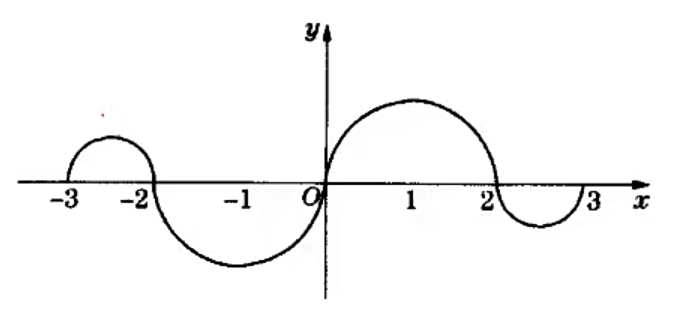
notion image
(A)
(B)
(C)
(D)

2.2.2 题型二 定积分计算

例1
例2
例3
例4 设
为正整数，证明：
例6 设
，计算
.
例7 设连续函数
在
内满足
，且
，则
.
例8
例9
例10 已知
连续,
, 求
的值.
例11 设
,
, 求
.
例12 若

2.2.3 题型三 变上限积分函数及其应用

  1. 连续性 设
  1. 在
  1. 上可积，则
  1. 在
  1. 上连续。
  1. 可导性定理 :设
  1. 在
  1. 上连续，则
  1. 在
  1. 上可导，
  1. 。
有
在一点处的可导性的结论
如果
在
上除点
外均连续，则在点
处
  1. 奇偶性 设
  1. 连续，则1.若
  1. 为奇函数，则
  1. 为偶函数。2.若
  1. 为偶函数，则
  1. 为奇函数。
例1 设
是奇函数，除
外处处连续，
是第一类间断点，则
是：
(A) 连续的奇函数；
(B) 在
间断的奇函数；
(C) 连续的偶函数；
(D) 在
间断的偶函数。
例2 设
，其中
则
在区间
内
(A) 无界
(B) 减
(C) 不连续
(D) 连续
例3 设
是连续函数，
是
的原函数，则
(A)
是奇函数
必是偶函数；
(B)
是偶函数
必是奇函数；
(C)
是周期函数
必是周期函数；
(D)
是单调函数
必是单调函数；
例4 设
是连续函数
的一个原函数，“
” 表示
的充分必要条件是
，则必有
(A)
是偶函数
是奇函数
(B)
是奇函数
是偶函数
(C)
是周期函数
是周期函数
(D)
是单调函数
是单调函数
例5 设函数
则( )
(A)
是函数
的跳跃间断点；
(B)
是函数
的可去间断点；
(C)
在
处连续但不可导；
(D)
在
处可导；
例6 设函数
连续，且
，求极限
例7 设
则
(A) 为正常数
(B) 为负常数
(C) 为0
(D) 不是常数
例9 设
在区间
上可导，
，且其反函数为
。若
，求
.
例11 设
连续，
，
。令
  1. 试证曲线
  1. 在
  1. 上是凹的。
  1. 当
  1. 为何值时，
  1. 取得最小值。
  1. 若
  1. 的最小值可表示为
  1. 。试求
  1. 。

2.2.4 题型四 积分不等式

积分不等式常用的方法
  1. 定积分不等式性质
  1. 变量代换
  1. 积分中值定理
  1. 变上限积分
  1. 柯西积分不等式
例1 设
,
, 则
(A)
.
(B)
.
(C)
.
(D)
.
I1 = \int{0}^{1} \frac{x}{2(1 + \cos x)} dx , I2 = \int{0}^{1} \frac{\ln (1 + x)}{1 + \cos x} dx , I3 = \int{0}^{1} \frac{2x}{1 + \sin x} dx , 则 ( )
例2 设
在
上连续，单调减。求证：
(
)
例3 设
在
上可导，且
，
。求证：
例4 设函数
在区间
上连续，且
单调增加，
。 证明：
f(x)
[a,b]
f(a) = 0
f(x)
[0,1]
f(0) = 0